Introduction to Partial Derivative Calculator
Partial derivative calculator with steps finds the derivative of a curve with numerous variables online. This partial derivatives calculator has the ability to differentiate a function numerous times.
Measuring the rate of change of the function with regard to one variable is known as partial derivatives in mathematics. It handles variables like x and y, functions like f(x), and the modifications in the variables x and y.
With a partial derivatives calculator, you can learn about chain rule partial derivatives and even more. To easily obtain the derivatives, a partial differentiation calculator can be used free online.
Process of using Second Order Partial Derivative Calculator
Partial differentiation calculator takes the partial derivative of a function by dividing the function into parts. Below is the process of using a partial differentiation calculator with steps.
How to give input:
- First, write a differentiation function or pick from examples.
- Now, from the drop-down list, choose the derivative variable.
- Next, decide how many times the given function needs to be differentiated.
- Press the calculate button to see the results.
The second partial derivative calculator will instantly show you step by step results and other useful metrics..
How does the Partial Differentiation Calculator show output?
The first partial derivative calculator uses derivative rules and formulas to evaluate the partial derivative of that function.
In results, it shows you the derivative (for calculating derivative of a function only, use derivative function calculator on home page. Apart from that, the second partial derivative calculator shows you possible intermediate steps, 3D plots, alternate forms, rules, series expansion and the indefinite integral as well.
Formulas used by Partial Derivative Calculator
The partial derivative of the function f(x,y) partially depends upon "x" and "y". So the formula for for partial derivative of function f(x,y) with respect to x is:
$ \frac{∂f}{∂x} = \frac{∂f}{∂u}\frac{∂u}{∂x} \;+\; \frac{∂f}{∂v}\frac{∂v}{∂x} $
Similarly, partial derivative of function f(x,y) with respect to y is:
$ \frac{∂f}{∂y} = \frac{∂f}{∂u}\frac{∂u}{∂y} \;+\; \frac{∂f}{∂v}\frac{∂v}{∂y} $
Solved example of Partial Differentiation Calculator
Suppose we have to find partial derivative of Sin(x4)
By putting values in calculator, we got solution:
$ \frac{d}{dx} sin(x^4) \;=\; 4x^3 cos(x^4) $
Conclusion
Partial differentiation calculator is a web based tool which works with mathematical functions along with multiple variables. Because of this, it becomes easy to solve and evaluate partial differentiation functions. The partial differentiation solver shows you different metrics and details which are essential for you to learn this concept.
Frequently Asked Questions
What are the benefits of using the first partial derivative calculator?
One of the major advantages of this calculator is accuracy. If you find derivatives manually, it is possible that you may get stuck in the middle of a maths problem and won't get rid of it for an hour. If you use a partial derivative tool it provides you an accurate result in a single click.
What is the chain rule in differential equations?
According to the chain rule, the derivative f (g (x)) equals f'(g (x)) g' (x). Partial derivatives Calculator uses the chain rule to differentiate composite functions.
Why is the partial derivative test of second order useful?
You could use second-order partial derivatives to identify whether the location is local maxima, minimum, or a saddle point. Once you've found the zero vector slope of the multivariate function, it indicates the tangent plane of the graph is smooth at that point.
Is partial differential equations hard?
Yes, the partial differential equations are hard to solve. But when these equations are converted into ordinary differential equations, we can evaluate them with different methods or by using a partial differential calculator.
What is the difference between ordinary differential equations and partial differential equations?
The ordinary differential equations (ODEs) are those equations where the derivatives are taken with respect to one independent variable. Whereas the partial differential equations (PDE’s) are those equations where the derivatives are taken with respect to more than one variable.
What are first order partial derivatives?
The derivative of a multivariable function with respect to an independent variable one time, is known as first order partial derivative. In partial derivatives, we differentiate a function with one variable by treating the other as a constant. We can use a first order partial derivatives calculator to solve them online.
What are continuous first order partial derivatives?
The partial derivative of a continuous function is known as continuous partial derivative if the derivative is also continuous. But for a continuous function, it is not necessary that its derivative should also be continuous.
What are elliptic partial differential equations?
A second order partial differential equation (PDE)
Auxx+2Buxy+Cuyy+Dux+Fuy+G=0 is considered an elliptic if, B2−AC < 0. Elliptic partial differential equations have no real characteristic surfaces.
What is the chain rule of partial differentiation?
The chain rule partial differentiation is a technique in which we differentiate a function with respect to two or three variables at a time.
For a function f=f(u,v), u=u(x,y) and v=v(x,y) the chain rule is,
$ \frac{df}{dx} \;=\; \frac{df}{du}\frac{du}{dx} \;+\; \frac{df}{dv}\frac{dv}{dx} $
And,
$ \frac{df}{dy} \;=\; \frac{df}{du}\frac{du}{dy} \;+\; \frac{df}{dv}\frac{dv}{dy} $
Use chain rule partial derivative calculator to differentiate chain rule partial differentiation online step by step.
















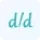
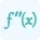
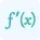
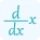






 Google Play
Google Play

0 Comment