Introduction to the Hessian Matrix Calculator
The Hessian matrix is a fundamental concept in calculus and optimization. It provides important information about the curvature of a function and helps determine critical points, extrema, and optimization paths. With the advent of technology, online tools known as Hessian matrix calculators have become increasingly popular. These calculators allow users to compute the Hessian matrix quickly and effortlessly.
Understanding the properties of the Hessian matrix can greatly enhance our ability to analyze and optimize functions. In this article, we will explore the concept of the Hessian matrix calculator, its formula, its working mechanism, and the benefits it offers.
Formula used by the Hessian Calculator with Steps
Before diving into the details of the Hessian calculator, let's understand the formula behind it. The Hessian matrix is a square matrix of second-order partial derivatives of a function. It provides essential information about the curvature of the function's graph, aiding in the identification of maximum, minimum, or saddle points. The formula for calculating the Hessian matrix involves taking the partial derivatives of each variable in the function.
The formula to calculate Hessian matrix is:

Where d²f/dx² represents the second partial derivative of f with respect to x, d²f/(dxdy) represents the second partial derivative of f with respect to x and y, and d²f/dy² represents the second partial derivative of f with respect to y. Use our partial derivative calculator to differentiate a multivariable function.
How Does the Hessian Matrix Calculator at a Point Work?
The Hessian matrix calculator at a point works by taking a user-provided function and evaluating it at a specific point to obtain the corresponding Hessian matrix. The calculator allows users to input the function and specify the values of the variables at the desired point. Once the input is provided, the calculator employs the formula discussed earlier to compute the Hessian matrix.
The calculator then displays the resulting Hessian matrix, providing insights into the second-order derivatives of the function at the given point. This information is valuable in various mathematical applications, such as optimization problems, determining concavity and extreme points.
How to Use the Hessian Matrix Calculator with Steps?
Using the Hessian matrix calculator is an easy process. Here's a step-by-step guide:
- Input the function you want to analyze and the point at which you wish to calculate the Hessian matrix.
- Click the "Calculate" or "Compute" button to trigger the computation process. The calculator will perform the necessary calculations and display the resulting Hessian matrix.
- Analyze the obtained Hessian matrix to gain insights into the function's behavior near the specified point. You can determine the concavity, convexity, and extrema based on the eigenvalues of the matrix.
To analyze the concavity and convexity of function, the knowledge of the second derivative test is required.
Why Use the Hessian Matrix Calculator Online?
There are several reasons to utilize an online Hessian matrix calculator:
Time and Effort Savings:
The calculator automates the complex mathematical calculations involved in finding the Hessian matrix, saving significant time and effort.
Accuracy and Error Reduction:
By using an online calculator, you can minimize human errors that may arise during manual computation.
User-Friendly Interface:
Online Hessian matrix calculator often provide a user-friendly interface, making it easier for users to input functions and interpret the results.
Benefits of Using the Hessian Derivative Calculator
The Hessian derivative calculator offers numerous benefits, including:
Optimization Analysis:
The Hessian matrix provides crucial information about the local behavior of a function, enabling optimization techniques to find the best possible solution.
Identifying Critical Points:
By analyzing the Hessian matrix, we can determine critical points such as maxima, minima, and saddle points.
Assessing Positive and Negative Definiteness:
The eigenvalues of the Hessian matrix allow us to assess whether a function is positively or negatively definite at a particular point.
How to Find the Hessian Matrix Calculator Online?
Finding an online Hessian matrix calculator is simple. Just follow these steps:
- Open your preferred search engine and enter relevant keywords such as "online Hessian matrix calculator."
- Review the search results and select a calculator from a reputable website or application. Check user reviews and ratings to ensure reliability.
- Some Hessian matrix calculators are available free of charge, while others may require a subscription or payment. Choose our calculator as it is free to use.
- Also, there are many other tools available on our derivative calculator website. All of these tools are also free to use.
In conclusion, the Hessian matrix calculator is a valuable tool for analyzing and optimizing functions. It simplifies the process of calculating the Hessian matrix, saving time and effort. By utilizing an online Hessian matrix calculator, you can enhance your understanding of function behavior and make informed decisions in optimization problems.
Frequently Asked Questions
What is the Hessian matrix?
The Hessian matrix is a square matrix of second-order partial derivatives of a function. It provides information about the concavity, convexity, and critical points of the function.
How is the Hessian matrix related to optimization?
The Hessian matrix plays a crucial role in optimization. It helps identify whether a critical point is a maximum, minimum, or saddle point, which aids in finding the optimal solution for a given problem.
Can the Hessian matrix be used for functions with multiple variables?
Yes, the Hessian matrix can be used for functions with multiple variables. It extends the concept of second derivatives to higher dimensions.




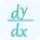
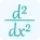
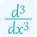
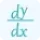












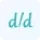
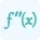
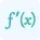
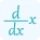



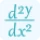
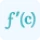



 Google Play
Google Play

0 Comment