Introduction to the Inflection Point Calculator
The points of inflection calculator is a valuable online resource created to aid individuals in understanding and identifying inflection points in mathematical functions. Whether you're navigating single-variable functions or more complex equations, this inflection points calculator streamlines the process of pinpointing inflection points – critical in analyzing the behavior of functions and understanding their curvature changes.
Understanding Inflection Point Calculator with Interval
Inflection points are key values within a function where the curvature transitions from concave upwards to concave downwards or vice versa. These points play a pivotal role in grasping the shape and behavior of a function, particularly in determining where it changes from being curved upward to curved downward, or the other way around.
The Formula used by the point of inflection calculator

The points of inflection calculator relies on the second derivative of a function to determine inflection points. The second derivative provides insights into the function's curvature behavior, helping identify where the curvature changes direction. Mathematically, if the second derivative changes sign at a point, that point is a potential inflection point.
Formula Used for the Example:
\[ \frac{d^2y}{dx^2} = 0 \]
This equation represents the second derivative of the function 'y' with respect to 'x'. The solutions of this equation give the x-values of potential inflection points.
Second Derivative Test for Inflection Points:
An inflection point occurs when the second derivative of the function changes sign. Mathematically, if the second derivative changes from positive to negative or from negative to positive at a specific point, that point is a potential inflection point. There are two conditions of the second derivative test for inflection points, such as;
- If f''(x) changes from positive to negative as x increases, there's a potential inflection point.
- If f''(x) changes from negative to positive as x increases, there's another potential inflection point.
It's important to note that an inflection point can also occur when the second derivative is zero (but doesn't change sign), or when the second derivative is undefined.
Working with the Concavity and Inflection Points Calculator
- Input the function you wish to analyze.
- Derive the first and second derivatives of the function with respect to 'x'.
- Set the second derivative equation to zero and solve for 'x'.
- The calculator will compute the 'x' values corresponding to potential inflection points.
- Further analysis may be required to confirm the inflection nature at these points.
Benefits of Using the Inflection Points Calculator
Efficiency: The calculator automates the calculation process, saving time and reducing the complexity of identifying inflection points.
Insightful Solutions: It provides a clear overview of where the curvature behavior of the function changes, aiding in understanding its overall shape.
Visualization: By locating inflection points, you gain insights into the points where the curvature transitions, allowing you to visualize the function's behavior.
Broad Applicability: The point of inflection calculator accommodates various functions and equations, making it useful for a wide range of mathematical scenarios.
Frequently Asked Questions
Why are inflection points important?
Inflection points offer insights into a function's behavior, aiding in understanding trends, extrema, and overall curvature changes in the graph.
How does the Inflection Point Calculator With Steps Work?
The calculator analyzes the second derivative of a function. It identifies points where the second derivative changes sign, indicating potential inflection points.
Can the calculator handle complex functions?
Yes, the points of inflection calculator is equipped to handle a wide range of functions, whether they're simple or complex. It swiftly calculates and analyzes the second derivative for accurate results.
Can I specify an interval for inflection point analysis?
Yes, you can define an interval to focus the analysis on a specific part of the function's domain. This is especially useful for pinpointing inflection points within a particular range.




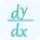
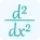
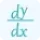












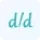
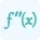
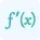
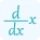


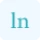

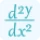
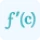



 Google Play
Google Play

0 Comment