Introduction to Tangent Line Calculator
The tangent line slope calculator is an advanced online tool that can assist you in calculating tangent lines. It uses the tangent line's slope to calculate the tangent line's equation. It needs just an input value to provide you with a tangent line. It allows you to save your time and energy from doing manual calculations.
The tangent line equation calculator is made by using the concept of derivatives. Because it uses a derivative formula to calculate the slope of the tangent line that gives the tangent line equation. Here, we introduce this tool so that you can easily calculate the equation of the tangent line without any manual calculations.
Formula used by Horizontal Tangent Line Calculator
The tangent line is a line that is drawn on the curve at the point of change. It represents the instantaneous rate of change at that point. The slope of the curve line at that point is calculated using derivatives. This slope is then used to calculate the equation of a tangent line. The equation of the tangent line calculator does these steps quickly to provide results within a few seconds.
The formula that this tool uses is expressed as;
$y-y_1=m(x-x_1)$
It is also written as,
$y=m(x-x_1)+y_1$
It is also known as the standard or slope-intercept form of the tangent line. Where (x1,y1) is the coordinate points on the curve. You can also use the normal line calculator, which provides you with the tangent line equation and the normal line equation.
The tangent line finder uses the above formula to provide you with the equation of a tangent line easily and quickly.
Tangent Line example
Let's calculate the slope of the line tangent at point $x_0=3$ to the curve $y=3x^2-5x+7$.
First we need to calculate the value of y at x0.
$y(x_0)=y(3)=3(3)^2-5(3)+7=$
$y(3)=3(9)-15+7=27-8=19$
We need to calculate the derivative of the given curve, which can be used to find the slope of the tangent line. So,
$y'(x)=\frac{d}{dx}(3x^2-5x+7)$
$y'(x)=6x-5$
The slope $m$ of the tangent line can be obtained by finding $y'(x_0)$. Therefore, substituting $x_0=3$ and,
$m=y'(3)=6(3)-5=18-5=13$
The equation of tangent line formula is,
$y=m(x-x_0)+y(x_0)$
Substituting the values of $m$ and $y(x_0)$ we get,
$y=13(x-3)+19$
Or,
$y=13x-20$
How to find the slope of the tangent line polar curve calculator?
Derivative calculator offers many online tools related to the derivative concept that can be easily found online. So you can easily find a tangent line calculator online by following these steps.
- Use the main keyword to search for the tool from your desired browser.
- Your search engine will provide you with different results. From these results, you can choose the tangent line equation calculator.
- On the website page, there will be a list of derivative tools.
Select the desired tool from the list. Or you can also use our different tools, such as the extreme point calculator, which helps you calculate maximum and minimum points.
How does the Tangent Line Finder Works?
The horizontal tangent line equation calculator works when you provide an equation of curve and a point. It uses the slope-intercept form of the equation of the straight line to find the tangent line equation at a specific point and provides a step-by-step complete solution.
When you provide an equation of curve with a tangent point to the line tangent calculator. It calculates the slope of the tangent line by finding derivatives of the given curve at the tangent point. After calculating the tangent line slope, the slope-intercept form is used.
Why use the Tangent of Parabola Calculator?
The derivative has many applications in calculus. One of the most critical applications is a linear approximation calculator. It approximates the function at the nearest point on the curve of a given function. Another derivative application is the tangent line, calculated using the rate of change. Since it contains tricky calculations, our vertical tangent line calculator makes it easy for you.
While calculating the tangent line equation, you must calculate the tangent's slope first. But you may need clarification because it is a very complex concept. We offer to use this calculator that allows you to do calculations without external help.
Benefits of using tangent line to the implicit curve calculator
This online calculator has many benefits. Some of these are listed here;
- It is easy to use because you have to follow some simple steps to use it.
- It is free of cost. You don't have to pay for other premium tools.
- It provides you with quick and 100% accurate results, so it is reliable.
- The tangent line to the implicit curve calculator helps you to learn more about the tangent line.
How to use a tangent line calculator with steps?
Our online calculator is advanced and easy to use. There are some simple and easy steps that you can use to perform the calculation on this tool. These steps are;
- In the first step, you need to enter the curve line function. In this step, you need to write the function for which you want to calculate the tangent line.
- Now enter the point to calculate the tangent line at that point.
- Review the function and click on the calculate button.
After clicking the calculate button, we will get the tangent line equation within a few seconds. It will also provide you with the curve function's derivative plot and all calculations. We hope that you find our tool helpful. You can also use our derivative graph calculator that provides you with the graph of the derivative of a function.
Frequently asked questions
How do you find the tangent line?
You can easily find the tangent line by using the general form of the tangent line equation. It is expressed as;
$y-y1=m(x-x1)$
What is the tangent line in trigonometry?
The tangent of an angle in trigonometry is the ratio of the lengths of the adjacent side to the opposite side. For the value of the cosine function to not be zero, it is the ratio of the sine and cosine functions of an acute angle.
Why do we use tangent lines?
We can determine the slope of a curved function at a specific location on the curve by using the tangent line, which is helpful. It is also essential to calculate the slope of a straight line.




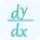
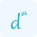
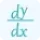












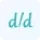


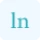

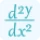
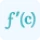



 Google Play
Google Play

0 Comment