Introduction to Directional Derivative Calculator
The directional derivative and gradient of a function at a particular point of a vector can be calculated using an online multivariable derivative calculator. This free gradient vector calculator also shows you how to calculate specific points step by step. Let's look at formulas and examples to discover how to find directional derivatives.
The direction of the multidimensional differential equation of a given vector v at a particular position x is intuitively deduced in mathematics. In calculus, It's the instantaneous rate of change of an implicit function traveling in x with v as its velocity. All other coordinates, on the other hand, remain constant.
But don't be confused between directional derivative and implicit derivative as these both are performed on implicit function. The rules of implicit differentiation is other than directional derivative. You can calculate implicit differentiation precisely using dy/dx calculator with steps.
Notations used by Directional Derivative Calculator
Let f be a curve with a tangent vector of v at a given location. Any of the following can be used in the directional derivative calculator to find a function f for p:
$ ∇_p \; f(x) $ $ f_p'(x) $ $ D_p \; f(x) $ $ D \; f(x) \; (p) $ $ ∇ \; f(x) $
The direction vector calculator uses these notations to compute the derivative of a function.
$ ∇_v f(x) \;=\; lim \; f(x+hv) \;-\; \frac{f(x)}{h} $
How Directional Derivative Calculator Works?
Follow these steps to get the gradient points and directional derivative of a given function using this online gradient vector calculator:
Input:
These are some simple steps for inputting values in the direction vector calculator in the right way.
- To calculate the directional derivative, Type a function for which derivative is required.
- Now select f(x, y) or f(x, y, z).
- Enter value for U1 and U2.
- Type value for x and y coordinate.
- Click the calculate button, to get output from a multivariable derivative calculator.
Output:
The directional derivative calculator calculates a function's derivative in the direction of two vectors therefore, it is also known as vector derivative calculator. The gradient is calculated by taking the derivative for every variable's function inputted in the direction vector calculator.
Solved Example of Directional Derivative
Find the directional derivative of x2y + xy2 with respect to x and y, where U1= 2 and U2 = -3.
Solution:
$ \frac{36}{13} \; \approx \; 9.9846 $
Conclusion
The partial derivative calculator with steps is used to estimate the slope in a single given variable's direction only, but the derivatives and gradients are calculated in three dimensions using an online derivative calculator with steps which is called a directional derivative calculator.
Finding the directional derivative and vectors requires graph paper, but it also raises the risk of errors. But the vector derivative calculator makes it easy for us, now we get the directional derivatives, utilize this free online gradient vector calculator, which delivers a step-by-step solution with 100 percent accuracy.
If you are struggling to find the linear approximation of a given function, try a differential approximation calculator. The online tool will instantly find the linear approximation step by step along with plot and possible intermediate steps.
Frequently Asked Questions
What is the significance of the direction's derivation?
The direction of the multidimensional differential function of a specified vector v at a particular position x is intuitively deduced in mathematics. It's the instantaneous rate of change of a function traveling at x with v as its velocity. Gateaux derivation is a specific case of directional derivation.
Differentiate between a directional and a second derivative?
The rate of change of a function in a certain direction is called the directional derivative. The directional derivative can be calculated using the gradient in the formula. But the second derivative is the derivative of the derivative. It measures the instantaneous rate of change of the first derivative of a function. For such calculations use online higher order derivative calculator with steps for precise calculation.
What is the definition of a direction gradient?
The direction of the gradient is the direction in which the function of p quickly rises, where magnitude of the gradient is the growth rate, and if the gradient of the function at the point "p" is not zero.
Find the directional derivative of x2y + xy2+ z2 with respect to x and y, where U1= 2, U2 = -3, and U3= -1 coordinate 2, -4, 3.
$ 15 \sqrt{\frac{2}{7}} \approx 8.01874 $
Is it possible for directional derivatives to be negative?
The directional derivative can be positive, negative, or zero as it is the change in direction. The function drops in this direction or grows in the opposite direction if the directional derivative is negative.
Is the derivative of the vector calculator accurate?
Yes, the derivative of the vector function calculator is accurate and error free. It takes your input and instantly provides you accurate step by step results.
Can I use a maximum directional derivative calculator in exams?
Most teachers recommend using derivatives of vector calculators for learning and practice. However, educational institutes do not allow using derivatives of vector function calculators. You have to solve equations in exams manually.
How to find a directional derivative calculator?
Simply search "derivative of a vector calculator" on Google to find the directional derivative calculator. You can click on our calculator in Google results.
Does directional derivatives calculator provide steps?
Yes, our derivative of a vector calculator provides step by step results along with visual representation.




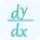
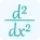
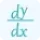












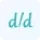
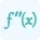
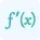
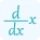


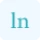

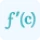



 Google Play
Google Play

0 Comment