Introduction to the Curvature Calculator
The Curvature Calculator is an efficient online tool designed to help you calculate curvature for various types of curves and functions. Whether you're dealing with 2D curves or exploring the curvature at a specific point, this calculator simplifies the process and provides valuable insights into the curvature of different shapes.
What is Curvature and Why is it Important?
Curvature refers to the amount by which a curve deviates from being a straight line. It plays a crucial role in fields like mathematics, physics, engineering, and even geography. Calculating curvature helps us understand the shape and behavior of curves, enabling us to determine whether a curve is more sharply bent or gently sloping.
How the Earth Curvature Calculator Works

Understanding how the curvature formula calculator functions is crucial for accurate results. It employs advanced mathematical algorithms to compute curvature based on the data you provide. Here's an overview of how it works:
Data Input: You input data points that describe the curve you're interested in. The more precise the data, the more accurate the result.
Tangent Line Approximation: The calculator approximates the tangent line at each data point. This tangent line represents the direction of the curve at that specific location.
Radius Calculation: Using mathematical techniques, the calculator calculates the radius of curvature for each point on the curve.
Curvature Computation: It then applies the formula (k = 1 / R) to compute the curvature at each point.
Visualization: Some Curvature Calculators also provide visual representations of the curve and its curvature profile for better comprehension.
Steps to Calculate Curvature Using the Calculator
Using the curvature of the earth calculator is straightforward:
- Enter the equation of the curve you want to analyze.
- Specify the variable(s) involved in the curve.
- Click the calculate button to obtain the curvature information.
Using the Curvature Formula Calculator for 2D Curves
The Curvature Calculator is versatile and can be used for 2D curves as well. It evaluates the curvature of the curve and provides insights into how sharply the curve is bending at different points.
Calculating Curvature at a Specific Point
With the Earth curvature calculator, you can calculate the curvature at a specific point on the curve. This is particularly useful when you want to understand the behavior of the curve at a particular location.
Formula Used by the Curvature Calculator at a Point
The Curvature Calculator employs a fundamental formula to calculate the curvature of a curve at a specific point. The formula is based on the derivatives of the curve's equation. Here's how it works:
Sure, here's the formula used by the curvature of curve calculator expressed in MathJax:
For a curve defined by the equation
\(y = f(x)\) \(\kappa\) \(P(x, y)\)
is calculated using the following formula:
\[ \kappa = \left| \frac{f''(x)}{\left(1 + (f'(x))^2\right)^{3/2}} \right| \]
Where:
f'(x) represents the first derivative of the curve's equation with respect to x.
f''(x) represents the second derivative of the curve's equation with respect to x.
For curves in parametric form, such as x = g(t), y = h(t) the formula is modified slightly:
\[ \kappa = \left| \frac{g'(t) \cdot h''(t) - g''(t) \cdot h'(t)}{(g'(t)^2 + h'(t)^2)^{3/2}} \right| \]
Where:
g'(t) and h'(t) represent the first derivatives of x and y with respect to t.
g''(t) and h''(t) represent the second derivatives of x and y with respect to t.
The Curvature Calculator applies these formulas, considering the appropriate derivatives, to calculate curvature accurately for different types of curves, including parametric curve and implicit curves.
Different Curvature Calculators for Different Needs
We've got special tools for special jobs:
- Finding the Bendiest Point Calculator
- Circle Size Finder for Curves Calculator
- Straight to Curvy: 2D Curves Calculator
- Pinpointing Bends: Point Curvature Calculator
- Earth's Roundness Calculator: Ev
How to find Curvature of Curve Calculator online?
You can easily find curvature of the earth calculator online by performing a simple web search. Many websites and software applications offer this tool for free or at a minimal cost. Make sure to choose a reputable source for accurate results.
Now that you've gained insights into the Curvature Calculator and its significance, you can start using it to explore the world of curves and bends.
Why to use Curvature Formula Calculator?
You might wonder why you should bother with a Curvature Calculator. Here are some compelling reasons:
Precision: Calculating curvature manually can be time-consuming and prone to errors. A Curvature Calculator ensures precision and accuracy.
Efficiency: It's much faster than manual calculations, making it a valuable tool for professionals with tight deadlines.
Visualization: Many calculators provide visual representations of the curve and curvature, aiding in understanding.
The calculator also caters to specific applications like calculating Earth's curvature. By inputting relevant parameters, you can determine the curvature of the Earth's surface over a certain distance. For more complex Earth curvature calculations, the Advanced Earth Curvature Calculator takes into account additional factors to provide accurate curvature information.
Frequently Asked Questions
Why is curvature important?
Curvature is essential in various fields like mathematics, physics, and engineering. It helps us analyze the shape of curves, determine maximum and minimum points, and even understand the behavior of physical objects in motion.
How does the calculator apply the curvature formula?
The curvature of curve calculator uses a well-defined formula that involves the derivatives of the curve. It analyzes how the curve's direction changes to determine the curvature at different points.
Is the Curvature Calculator accurate?
Yes, the curvature of the earth calculator is accurate and reliable. It employs sophisticated algorithms to ensure precise calculations of curvature for various types of curves.




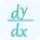
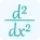
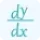












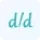
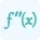
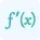


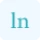

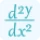
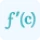



 Google Play
Google Play

0 Comment