Introduction to the logarithmic differentiation calculator
Logarithmic differentiation is a powerful mathematical technique used to find derivatives of complex functions involving logarithmic expressions. While the manual computation of such derivatives can be time-consuming and there are many chances of getting wrong solutions. We introduce an online logarithmic implicit differentiation calculator that simplifies the process significantly. In this article, we will explore the concept of logarithmic differentiation, understand the formula used by the derivative of the log function calculator, learn how to use it effectively, and discuss the benefits it offers.
Formula used by the derivative of log function calculator
Logarithmic differentiation is a type of differentiation which is used to calculate the rate of change of the logarithmic functions. This calculator uses the derivative rules for finding the derivative of logarithmic functions. According to these rules, if f(x) = ln(g(x)),
$\frac{d}{dx} [\ln(g(x))] = \frac{g'(x)}{g(x)}$
Where g'(x) is the derivative ln(g(x)) without log. This formula allows us to solve complex calculus problems and understand how the rate of change occurs. You can also use our implicit derivative calculator which uses the above formula to calculate derivatives of implicit functions.
How Does an Online Logarithmic Differentiation Calculator Work?
The differentiation of the log function calculator simplifies the process of finding derivatives of logarithmic functions. This calculator is equipped with advanced algorithms that handle complex mathematical calculations. It takes the input function from the user and applies the logarithmic differentiation technique to find the derivative.
The calculation process involves several steps. First, the calculator identifies the logarithmic functions within the input expression. It then applies the logarithmic differentiation formula to each logarithmic function separately. After finding the derivative of each logarithmic function, the calculator combines the results to provide the final derivative of the entire expression.
How to Use a Derivative of Logarithmic Function Calculator?
Using a derivative of a logarithmic function calculator is simple and user-friendly. Here is a step-by-step guide to use this calculator effectively:
- Open the logarithmic differentiation calculator in your web browser.
- Identify the logarithmic function for which you want to find the derivative.
- Enter the function in the provided input field. Make sure to use the appropriate base for the logarithmic function.
- Review the entered function for any errors.
- Click on the "Calculate" button to start the calculation process.
After clicking the calculate button, the calculator will display the derivative of the logarithmic function as the output. By following these simple steps, you can quickly obtain the derivative of a logarithmic function without the need for manual calculations. Use our differentiation calculator to find the rate of change in an easy way.
Why Use a Logarithmic Differentiation Calculator with Steps?
A derivative of the log function calculator that provides steps offers several advantages. First and foremost, it allows you to verify the accuracy of the calculated derivative by following the step-by-step process. This feature is particularly helpful when learning or teaching logarithmic differentiation, as it enables a deeper understanding of the underlying concepts.
Additionally, the step-by-step functionality of the calculator assists in error detection and correction. By breaking down the derivative calculation into individual steps, it becomes easier to identify and rectify any mistakes made during the process.
Benefits of using an online derivative of ln function calculator
Utilizing an online derivative of the ln function calculator offers numerous benefits. Some of the key advantages include:
Time-saving:
The calculator provides instant results, saving valuable time compared to manual calculations.
Accuracy:
The calculator performs precise calculations, minimizing the possibility of human error.
Convenience:
As an online tool, the calculator is accessible from anywhere with an internet connection.
Educational tool:
The calculator can serve as an educational resource, aiding students and enthusiasts in learning logarithmic differentiation.
Free availability:
Many online logarithmic differentiation calculators are available at no cost, making them easily accessible to all.
How to find a logarithmic differentiation step-by-step calculator?
Finding a logarithmic differentiation step-by-step calculator is simple. Search for "logarithmic differentiation calculator with steps" or a similar phrase in your preferred search engine. This query will provide you with several online calculators that offer detailed step-by-step solutions for finding the derivative of logarithmic functions. Choose one that suits your requirements and start exploring the fascinating world of logarithmic differentiation.
In conclusion, the logarithmic differentiation calculator is a valuable tool for finding derivatives of logarithmic functions quickly and accurately. Whether you're a student, educator, or simply someone in need of precise derivatives, this online calculator can simplify your mathematical tasks. By utilizing its functionality and step-by-step approach, you can enhance your understanding of logarithmic differentiation and save time in the process.
Frequently Asked Questions
Why do you use logarithmic differentiation?
Logarithmic differentiation is a technique of solving derivatives of logarithmic functions. This technique involves different derivative rules such as chain rule and product rule of derivative. This technique is important to find rate of change of a log function because we can’t calculate such derivatives with the usual differentiation methods.
Is the logarithmic differentiation calculator reliable?
Derivative of ln function calculators are reliable tools that provide accurate results when used correctly.
What is an example of a logarithmic function derivative?
For example, if we want to find the derivative of ln(x) at x = 3, we can substitute x = 3 into the derivative formula:
d/dx [ln(3)] = 1/3
So, at x = 3, the derivative of ln(x) is equal to 1/3. This tells us that the slope of the tangent line to the graph of ln(x) at x = 3 is 1/3. Similarly, we can find the derivatives of other logarithmic functions using the logarithmic differentiation formula.




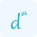
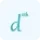
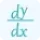












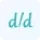
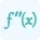
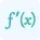
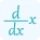


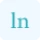




 Google Play
Google Play

0 Comment