Introduction to the Taylor Series Calculator
The Taylor series calculator is a powerful mathematical tool widely used in calculus and various scientific disciplines. It allows us to approximate complex functions with polynomials, providing accurate results that are essential for various applications in engineering, physics, economics, and more.
In this article, we will delve into the concept of Taylor Series, understand how the calculator works, explore its applications, and discover the benefits it offers. Whether you are a student or a professional, understanding the Taylor series calculator with steps can significantly enhance your problem-solving capabilities.
Taylor Series Expansion Formula
The Taylor Series Expansion Formula is the key to using the calculator effectively. It uses the concept of differentiaiton to approximatioe a function. So, to find series expansion of a function, we need to first calculate derivatives of a function up to nth order. It can be expressed as:
$f(x)=f(a)+f’(a)(x-a)+\frac{f’’(x)(x-a)^2}{2}+\frac{f’’’(x)(x-a)^3}{3}+...$
where:
f(x) is the original function
f(a) is the value of the function at the point
f’(a) is the first derivative of the function
f’’(a) is the second derivative of the function
f’’’(a) is the third derivative of the function
… represents the higher-order derivatives.
This formula is used by the multivariable Taylor series calculator. According to the above formula, the higher derivatives of f(x) are important to find series expansion. Try our nth derivative calculator online that helps you to find higher order derivatives of a function easily just in a single step.
Examples of Approximating Functions with Taylor Series
Let's explore a couple of examples to demonstrate the effectiveness of the Taylor Series Calculator:
Example 1: Approximating sin(x) near x=0
Using the Taylor Series Expansion for sin(x) around x=0, we get:
$\sin(x)\approx x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+...$
By using different numbers of terms, you can observe how the approximation approaches the original sine function as x gets closer to 0.
Example 2: Approximating e^x near x=1.
Using the Taylor Series Expansion for e^x around x=1, we get,
$e^x \approx e -e(x-1)+\frac{e}{2}(x-1)^2+\frac{e}{6}(x-1)^3+\frac{e}{24}(x-1)^4+...$
Here the derivative of e^x is equal to e^x itself. This approximation tells the behavior of e^x near x=1.
How the Calculator Approximates Functions Using Polynomials
The Taylor Polynomial Calculator uses algorithms to perform the approximation process efficiently. Here's how it works:
Input Function and Point:
You provide the calculator with the function you want to approximate and the point around which you want to perform the approximation.
Calculating Derivatives:
The calculator automatically calculates the derivatives of the function up to a certain order at the specified point. This step involves a series of mathematical operations to compute the derivatives accurately.
Constructing the Polynomial:
Using the derivatives obtained in the previous step, the calculator constructs the Taylor Polynomial by applying the Taylor Series Expansion Formula. The number of terms used in the polynomial determines the accuracy of the approximation.
Evaluating the Polynomial:
The calculator evaluates the polynomial for various values of x within the chosen range. This process generates a set of points that lie on the polynomial curve.
Visual Representation:
The calculator then plots the original function and the Taylor Polynomial on the same graph. This visual representation allows you to compare the two functions and assess the accuracy of the approximation. Find the series expansion graph with derivative graph calculator.
How to use Taylor Series Approximation Calculator?
Using a Taylor Series Approximation Calculator is simple and efficient. Follow these steps:
Input the function
Enter the function that you want to approximate using the Taylor series.
Specify the center of expansion
Choose the point around which you want to expand the Taylor series. This point is crucial in determining the accuracy of the approximation.
Select the number of terms
Decide how many terms you want to include in the Taylor series. More terms usually result in a more precise approximation.Get the approximation
Once you have provided the necessary information, the calculator will generate the Taylor series approximation for your function.
Benefits of using Taylor Series Expansion Calculator
The Taylor Series Expansion Calculator comes with a plethora of benefits that make it indispensable for anyone dealing with complex functions:
- Precision: The Taylor series expansion provides a precise approximation of functions, ensuring accurate results.
- Speed and Efficiency: Calculating Taylor series manually can be time-consuming and prone to errors. The calculator offers rapid and error-free solutions.
- Simplicity: With just a few clicks, users can obtain detailed Taylor series expansions that would otherwise require laborious calculations.
- Education and Research: The calculator serves as a valuable educational tool, enabling students and researchers to explore various functions and their approximations.
- Wider Applicability: The Taylor series expansion technique is applicable to a wide range of functions, making the calculator useful across diverse fields.
How to find a Multivariable Taylor Series Calculator online?
Finding a reliable Multivariable Taylor Series Calculator online is crucial for dealing with functions of multiple variables. Here's how you can find one:
- Search Engines:Use popular search engines to look for "Multivariable Taylor Series Calculator" or "Multivariate Taylor Series Calculator."
- Visit reputable mathematical websites that provide a wide range of mathematical tools, including Taylor series calculators.
- Many universities offer online resources and calculators related to calculus and mathematics.
- Check app stores for mobile applications that provide multivariable Taylor series calculations.
- Ensure that the calculator you choose is reliable, accurate, and user-friendly to obtain precise results.
FAQs
Can the Taylor series be used for any function?
Taylor series can only be used for analytic functions, meaning functions that can be expressed as infinite power series. Non-analytic functions may not have a valid Taylor series representation.
How do I know the Taylor series approximation is accurate enough for my needs?
The accuracy of the Taylor series approximation depends on the number of terms used. Adding more terms will result in a more accurate approximation. You can also validate the results using other methods or known solutions.
Are there Taylor series calculators available for mobile devices?
Yes, there are Taylor series calculator applications available for both Android and iOS devices. These apps provide convenience and ease of use for on-the-go calculations.
Can I use Taylor series to approximate transcendental functions like sine and cosine?
Yes, Taylor series can be used to approximate transcend




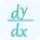
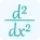
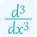












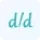
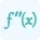
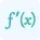
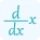


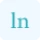

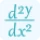
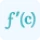



 Google Play
Google Play

0 Comment