Introduction to the Mean Value Theorem Calculator
The Mean Value Theorem is a fundamental concept in calculus, introduced by the legendary mathematician Augustin-Louis Cauchy. It establishes a profound relationship between the average rate of change of a function over an interval and its instantaneous rate of change at a specific point within that interval. While grasping the theorem's essence is crucial for understanding calculus, applying it practically can sometimes be challenging.
This is where the mean value theorem calculator comes into play. It's a valuable tool that simplifies complex calculations and provides quick solutions, making it an indispensable aid for students, teachers, and anyone dealing with calculus.
Exploring How the Mean Value Theorem Solver Works
Think of the mean value calculator as a smart helper. It uses a special formula that helps explain how the theorem works. All you need to do is put in the right numbers, and it will give you an answer that shows how things change on average. Plus, it's not just about numbers – it also helps you see how this math stuff applies to real situations in the world.
Practical Applications and Use Cases
Discover the practical implications of the Mean Value Theorem in various fields, from physics to economics. This theorem has a role in all sorts of areas, from understanding the movement of objects to predicting economic trends. The calculator helps you see how these ideas are connected.
Utilizing the Mean Value Theorem for Derivatives Calculator
If you're feeling a bit unsure about using the calculator, don't stress. We've got your back. Our step-by-step guide will walk you through the whole process. It's like having a friend who explains everything – from typing in your math problem to figuring out the answer.
Obtaining Results and Interpretation
The Mean Value Theorem Calculator not only gives you numerical results but It actually tells you what those numbers mean

Formula used by the Mean Value Theorem Calculator with Steps
The mean value theorem solver operates based on a specific formula that unveils the insights behind the theorem. This formula is designed to simplify the process of calculating the mean value of a function over a given interval. Let's break down the formula and the steps involved:
Step 1: Choose Your Function
Start by selecting the function you want to analyze. This could be any mathematical expression that represents a relationship between variables.
Step 2: Identify the Interval
Specify the interval over which you want to calculate the mean value. This interval is defined by two points, typically denoted as a and b, where a<b.
Step 3: Apply the Formula
The formula used by the mean value theorem calculator is based on the average rate of change concept:
\[ f'(c) = \frac{f(b) - f(a)}{b - a} \]
Here, f'(c) represents the instantaneous rate of change at a specific point c within the interval [a, b]. The formula calculates this rate of change by comparing the function values at the endpoints a and b, and then dividing by the length of the interval [b - a]. The above formula is an application of derivatives which is used to calculate the mean value of a function. You can also use our derivative calculator to find the rate of instantaneous change in a function.
Step 4: Calculate the Instantaneous Rate of Change
Plug in the values of f(a) and f(b) from your chosen function into the formula. Evaluate f'(c) to find the instant rate of change at point c.
Step 5: Interpretation
The calculated f'(c) represents the slope of the tangent line to the function at point c. This slope is equal to the average rate of change of the function over the interval [a, b]. This key insight lies at the heart of the Mean Value Theorem's application.
By following these steps and using the formula, the mean value calculator breaks down complex calculations into manageable steps, making the theorem's principles accessible and understandable.
Why Use a Calculator for Mean Value Theorem?
Now, doing calculations for the Mean Value Theorem can be a bit tricky, especially when dealing with complicated functions. But don't worry, that's where our mean theorem calculator steps in. It makes things easier by breaking down the steps for you, so you can really understand what's going on.
The Mean Value Theorem is not just another mathematical concept; it has far-reaching applications in various fields. Here's why you should consider using the Mean Value Theorem and its calculator:
Problem Solving: It's a potent tool for solving problems related to motion, rates, and more, making it indispensable in physics, engineering, and economics.
Enhanced Understanding: Utilizing the calculator helps you gain a deeper understanding of the Mean Value Theorem's practical applications.
Time Efficiency: Saves time on lengthy manual calculations, allowing you to focus on the core concepts.
Advantages of Using our Average Value Theorem Calculator
Our Mean Value Theorem Calculator offers multiple benefits:
- Simplicity: Complex calculations simplified into user-friendly steps.
- Accuracy: Precise results without the risk of manual errors.
- Accessibility: Access the calculator anytime, anywhere, free of charge.
- Comprehensive Explanation: Understand the logic behind the calculations.
Frequently Asked Questions
How does the Mean Value Theorem Solver work?
Our calculator employs the Mean Value Theorem formula to determine the point where the instant rate of change equals the average rate of change. By inputting the function and interval, the calculator breaks down the calculation steps for you.
How accurate are the results provided by the calculator?
The calculator provides precise results based on the input you provide. It breaks down the calculation steps, ensuring accuracy and transparency in the process.
Can the calculator handle complex functions?
Yes, the calculator can handle a wide range of functions, including complex ones. It simplifies the process by guiding you through the steps to calculate the Mean Value Theorem.
Why is the Mean Value Theorem for Derivatives Important?
The Mean Value Theorem bridges the gap between average and instantaneous rates of change, providing insights into real-world scenarios like motion and economics. It serves as a crucial tool in understanding the behavior of functions.




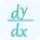
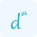
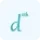
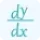












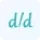
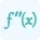
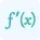


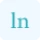

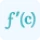



 Google Play
Google Play

0 Comment