Introduction to Derivative Definition Calculator
The limit definition of a derivative calculator is an online tool that calculates the rate of change of a function using the first principle of differentiation. The calculations of derivatives by definition manually are complex and tricky. This tool allows you to differentiate a function by using first principle in an easy and quick way.
Calculus studies a continuous rate of change that involves derivatives and integration. Derivative calculator helps you to calculate the rate of change of a function due to the change in an independent variable. But it takes work to calculate the derivative of a function by definition. Therefore, we introduce you to an online tool that helps you quickly determine a function's derivative.
The formula used by Definition of a Derivative Calculator
The derivative, by definition, is the central concept in differentiation. It is defined by the rate of change in a function due to the change in its independent variable. In other words, it is also known as the slope of the tangent line at the point where the graph of a function changes. The derivative by definition formula is expressed as;
$f'(x)=\lim_{x\to0}\frac{f(x+\delta x)-f(x)}{\delta x}$
Where,
- δx=is the change in x.
- f(x+δx)=is the change in f(x) due to the change in x.
- f(x)=is the original function.
- f'(x)=is the derivative of f(x).
The use of the derivative definition calculator provides you with easy and quick solutions. So you can avoid long-term calculations. To learn more about derivatives, you can use the directional derivative calculator, which gives you the derivative of a function in a specific direction.
Derivative definition example
Let's calculate the derivative of $y=\sqrt{x}$ by using the limit definition of derivatives.
$y=\sqrt{x}$
For a change in x variable, there will be a change in the function also. So, substituting, x=x+δx and y=y+δy.
$y+\delta y=\sqrt{x+\delta x}$
$\delta y=\sqrt{x+\delta x}-y$
Since,
$y=\sqrt{x}$
therefore,
$\delta y=\sqrt{x+\delta x}-\sqrt{x}$
Now dividing both sides by δx, we get
$\frac{\delta y}{\delta x}=\frac{\sqrt{x+\delta x}-\sqrt{x}}{\delta x}$
By the limit definition of derivatives, for δx>0, taking the limit as δx approaches zero.
$\lim_{\delta x\to 0}\frac{\delta y}{\delta x}=\lim_{\delta x\to 0}\frac{\sqrt{x+\delta x}-\sqrt{x}}{\delta x}$
Since,
$lim_{\delta x\to 0}\frac{\delta y}{\delta x}=f'(x)$
Therefore, simplifying the above limit.
$f'(x)=\lim_{\delta x\to 0}\frac{\sqrt{x+\delta x}-\sqrt{x}}{\delta x}\times\frac{\sqrt{x+\delta x}+\sqrt{x}}{\sqrt{x+\delta x}-\sqrt{x}}$
$f'(x)=\lim_{\delta x\to 0}\frac{(x+\delta x)-x}{\delta x(\sqrt{x+\delta x}+\sqrt{x})}$
More simplification,
$f'(x)=\lim_{\delta x\to 0}\frac{\delta x}{\delta x(\sqrt{x+\delta x}+\sqrt{x})}$
Or,
$f'(x)=\lim_{\delta x\to 0}\frac{1}{\sqrt{x+\delta x}+\sqrt{x}}$
Substituting the limit, we get
$f'(x)=\frac{1}{\sqrt{x+0}+\sqrt{x}}=\frac{1}{\sqrt{x}+\sqrt{x}}$
$f'(x)=\frac{1}{2\sqrt{x}}$
So the derivative of sqrt x is $\frac{1}{2\sqrt{x}}$. Also use our linear approximation calculator to linearize a funciton at a specfic point.
How to find First Derivative using the Limit Definition Calculator?
Finding the definition of derivative solver involves a few simple steps that help to find this tool online. These steps are:
- Open your preferred browser and activate it to the search engine google.
- On google, search for derivative definition calculators. It will provide you with a list of different websites. Or you can also write the full URL of this website.
- By choosing our derivative calculator, you can also use different tools such as product rule calculator. It uses the product rule formula to provide you the derivative of a function.
How does the Derivative using Definition Calculator work?
The limit definition of the derivative calculator with steps works when an input function is provided. It uses the limit definition of derivatives in the backend to evaluate the derivative of a function. It helps you by providing a complete step-by-step solution. It also explains every single step involved in the solution.
When you input a function to the derivative calculator using definition, it analyzes the function and checks whether it is differentiable and continuous. It is because the continuity of a function is a key factor to find its rate of change. After analyzing the function, our advanced derivative tool provides an accurate and quick result.
Why to use the definition of the derivative calculator?
The derivative calculator offers an advanced and excellent tool to make calculating derivatives easier for you. Using this tool, you can learn the rate of change of a function and the derivative graph. So, it would be best for you to use this online calculator.
While doing calculations of derivatives, by definition, is a lengthy and tricky process. The derivative-by-definition method is more challenging than using derivative rules. Moreover, it also involves the concept of limit. But using a derivative calculator can save you from doing these manual calculations.
Benefits of using limit definition of derivative calculator with steps
The derivative calculator using definition has many benefits that you can get by using it. All you need is a good internet connection and some simple clicks. Some other benefits of using this calculator are;
- It is easy to use because you need to perform some simple steps and help to calculate the first derivative of a function.
- Finding derivative using definition calculator is free, so don’t pay for other premium tools.
- It allows you to learn more about derivatives by providing a step-by-step solution.
- It provides you with a quick and 100% accurate solution.
- It can handle any input function. For example, if you give a combination of two functions, it calculates the derivative using the chain rule calculator.
How to use the definition of derivative at a point calculator?
Using this calculator online can save you from doing long and tricky manual calculations. It is easy to use this calculator because it just requires an input value. Use the following steps to calculate the limit definition of a derivative calculator.
- In the first step, you need to enter the function. This step requires a function for which you want to calculate the rate of change four times.
- Now select the variable by which you want to differentiate the given function.
- Review the function and click the calculate button.
After Clicking the calculate button, the derivative definition calculator will provide you with the solution within a few seconds.
Frequently asked questions
What is a simple Definition of derivative?
In mathematics, derivative is the rate of change of a function with respect to a variable. It provides fundamental solutions of problems in calculus and differential equations.
What is the first Definition of derivative?
Since derivative is simply a measure of rate of change in a function. For example, it can be the rate of change of distance with respect to time. The first definition of derivative says that, if there is a change in a variable, then it will make change in the function also.
What are the 3 derivative rules?
The three most common rules of derivatives are;
- Power rule
- Product rule
- Quotient rule




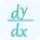












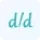
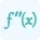
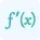






 Google Play
Google Play

0 Comment