Introduction to the Critical Points Calculator
The critical point calculator is a valuable online tool designed to help you determine critical points of multivariable functions effortlessly. Whether you're dealing with a single function or multiple variables, this calculator streamlines the process of identifying critical points, which are pivotal in calculus and optimization.
Understanding Critical Points
Critical points are significant values in a function where its derivative is either zero or undefined. These points play a crucial role in understanding the behavior of a function, especially when it comes to finding extrema (maximum or minimum values) and saddle points.
Formula Used by Critical Points of Multivariable Functions Calculator

The formula used by the critical point calculator to identify critical points in a function involves the calculation of the derivative(s) and the subsequent analysis of these derivatives. The primary goal is to find the points where the derivative(s) of the function become zero or undefined. These points are potential candidates for critical points.
For a function f (x) of a single variable, a critical point is typically found where the first derivative f′ (x) equals zero or is undefined. Mathematically, this can be expressed as:
f′ (x) = 0 or f′ (x) is undefined
For a function f (x,y) of two variables, critical points are determined by finding values of x and y where both partial derivatives ∂f/∂x and ∂f/∂y are either zero or undefined:
- ∂f/∂x= 0 or ∂f/∂x is undefined
- ∂f/∂x = 0 or ∂f/∂y is undefined
For functions with more variables, the process is extended to include an additional partial derivatives calculator with respect to those variables.
The calculator employs these fundamental principles to determine critical points in various types of functions. It evaluates derivatives, examines their values, and identifies points where they meet the criteria of being zero or undefined.
How the critical points with constraints calculator Works
Now that we have a basic understanding of the formula, let's explore how the critical points of a function calculator handles this complex process seamlessly. This online tool automates the differentiation and equation-solving steps, making it exceptionally user-friendly.
Here's a brief overview of its operation:
- Input Function: Users input their mathematical function into the calculator.
- Automatic Differentiation: The calculator computes the derivative of the function.
- Equation Solving: It sets the derivative equal to zero and finds the solutions.
- Displays Critical Points: The calculator then displays the critical points of the function.
Using the Critical Points Derivative Calculator: Step-by-Step
- Enter the function you want to analyze.
- Specify the variables involved in the function.
- If applicable, input any constraints or intervals for analysis.
- Hit the calculate button to reveal the critical points and associated information.
Benefits of using the Critical Points of a Function Calculator
- Efficiency: The calculator swiftly handles complex calculations that could be time-consuming manually.
- Accuracy: Algorithms ensure precise identification of critical points and their characteristics.
- Step-by-Step Insight: The calculator often provides detailed steps, aiding in understanding the process.
- Multiple Variables: It accommodates functions with two or three variables, broadening its applicability.
How to Find Critical Point Calculator Online?
Accessing a critical points of multivariable functions calculator is as easy as a quick internet search. Numerous websites and mathematical tools offer this service for free. Simply type 'Critical Points Calculator' into your preferred search engine, and you'll have multiple options to choose from.
Frequently Asked Questions
What are critical points?
Critical points are values in a function where the derivative is zero or undefined.
Can the calculator handle functions with constraints?
Yes, the calculator can identify critical points even when constraints are involved.
How does the calculator deal with multivariable functions?
The calculator adeptly manages functions with two or three variables, offering comprehensive results.
Are saddle points considered by the calculator?
Absolutely, the calculator detects both maximum and minimum points as well as saddle points.




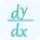
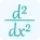
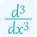
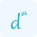
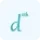
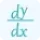












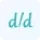
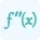
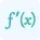



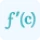



 Google Play
Google Play

0 Comment