Introduction to Second Implicit Derivative Calculator
The second implicit derivative calculator is an online tool with which you calculate the second derivative of an implicit function. It uses the concept of implicit differentiation and provides you with accurate results. For this, it only requires an input value as a function.
In mathematics, implicit differentiation is a derivative used to calculate the derivative of a function defined implicitly. Sometimes, you need to calculate the second implicit derivative of a function. Therefore, we offer you an online tool that calculates second implicit derivatives quickly.
Formula used by second implicit derivative calculator with steps
In calculus, implicit differentiation is a concept used to find the rate of a change of an implicit function. It follows all of the derivative rules to calculate 2nd implicit differentiation.
Related: Use an online implicit derivative calculator on this website for free!
The d^2y/dx^2 calculator does not use a specific formula to calculate the second derivative. It computes the derivative according to the given function and repeats it two times to calculate the second derivative. It uses the following steps to find a solution.
- It applies the differentiation on both sides of the implicit equation.
- It computes derivatives by using differentiation rules.
- Separating each term with respect to variables.
- Rearranging the equation in terms of dy/dx.
- Applying derivative again to calculator second derivative.
The formula of the second implicit derivative calculator is based on the limit definition of derivatives. It is given by,
$\frac{dy}{dx}=\lim_{h\to 0}\frac{f(x+h)-f(x)}{h}$
The second parametric derivative calculator provides you with a quick result without performing above long-term calculations. You can also use the chain rule to calculate the derivative of an implicit function.
For specific calculations, use the chain rule differentiation calculator on this website.
Second Implicit Derivative example
Let's calculate the derivative of x^2y. For this, suppose that,
$y=x^2y$
Differentiating both sides with respect to x, we get
$\frac{dy}{dx}=\frac{d}{dx}(x^2y)$
By using the product rule of derivative calculator,
$\frac{dy}{dx}=x^2.\frac{dy}{dx}+2xy$
Now rearranging the equation,
$\frac{dy}{dx}-x^2\frac{dy}{dx}=2xy$
$(1-x^2)\frac{dy}{dx}=2xy$_______(A)
Or,
$\frac{dy}{dx}=\frac{2xy}{1-x^2}$
Differentiating (A) again with respect to x,
$\frac{d}{dx}\left((1-x^2)\frac{dy}{dx}\right)=\frac{d}{dx}(2xy)$
$\frac{d}{dx}\left(\frac{dy}{dx}-x^2\frac{dy}{dx}\right)=2y+2x\frac{dy}{dx}$
$\frac{d^2y}{dx^2}-2x\frac{dy}{dx}-x^2\frac{d^2y}{dx^2}=2y+2x\frac{dy}{dx}$
More simplification,
$(1-x^2)\frac{d^2y}{dx^2}-4x\frac{dy}{dx}=2y$
Since $\frac{dy}{dx}=\frac{2xy}{1-x^2}$,
$(1-x^2)\frac{d^2y}{dx^2}-4x\cdot\left(\frac{2xy}{1-x^2}\right)=2y$
Multiplying by $(1-x^2)$,
$(1-x^2)^2\frac{d^2y}{dx^2}-8x^2y=2y(1-x^2)$
$(1-x^2)^2\frac{d^2y}{dx^2}=2y-2x^2y+8x^2y$
$(1-x^2)^2\frac{d^2y}{dx^2}=2y+6x^2y$
Hence by rearranging, we get the second implicit derivative of x^2y, which is,
$\frac{d^2y}{dx^2}=\frac{2y+6x^2y}{1-x^2}$
This calculator is reliable to find the derivative of parametric funcitons in an easy and advanced way.
How to find the d^2y/dx^2 Calculator online?
Finding an online tool to find implicit derivatives of a function requires some simple steps. We provide you a list of some easy steps that will help you to find our tool. These steps are given by:
- Open your preferred browser such as chrome or firefox. Navigate your browser to the search engine google.
- Now search for our website, derivative calculator on google. Or, you use the URL to access our online tools.
- On the website page there will be a list of different derivative tools. Select the double implicit differentiation calculator.
How is the Second Implicit Differentiation Calculator?
Working of the implicit second derivative calculator depends on an input function that is collected from the user. It uses the derivative formula along with all differentiation rules in the backend to provide you a step-by-step complete solution. It is an advanced derivative tool that is capable of identifying an implicit function.
When you provide a function as an input, this tool analyzes the function. It determines that either the function is implicit or explicit. After analyzing the function, the implicit differentiation d^2y/dx^2 calculator differentiates it twice and provides a step-by-step solution quickly.
Why to use implicit differentiation second derivative calculator?
In mathematics, derivatives play an essential role in calculating the rate of change. It helps to calculate tangent lines, maxima and minima, and many other terms. It also has many applications in real-life problems. For example, it helps to determine the profit and loss in business using a derivative graph.
Implicit differentiation is also an essential concept in calculus. It deals with studying the rate of change of an implicit function. But the calculations of the implicit derivative are complex, unlike an ordinary derivative. Therefore it would be best for you to use a second implicit differentiation calculator.
Benefits of using second derivative implicit differentiation calculator
The advanced implicit second derivative calculator calculates the second derivative of a function by using implicit differentiation solver. It has numerous benefits that you can get by using it. Some of these are:
- It is simple to use because only a few easy steps are required.
- Because it is free, there is no need to pay for other premium tools.
- It gives you a step-by-step solution, enabling you to learn more than derivatives.
- Double implicit differentiation calculator gives you a quick and correct answer.
- Any input function that you provide can be handled by it. For example, if you provide a product of two functions, the product rule calculates the derivative.
How to use a second derivative implicit differentiation calculator?
The use of an online tool is a quick and easy way to do calculations. So, to find the second implicit derivative, you can use our best calculator. For this, use the following steps.
- In the first step, you need to enter the function. This step requires an implicit equation for which you want to calculate the rate of change.
- Now select the variable by which you want to differentiate the given function.
- Now select a number from the time menu. You can select how many times you want to differentiate a function in this step. You can also select 2 to calculate the 2nd derivative.
- Review the function and click the calculate button.
After clicking the calculate button, you will get the second-order implicit derivative within a few seconds. Also, this tool will provide the derivative graph so that you can visually determine the rate of change. Or, you can also use our derivative grapher to visualize the rate of change in any function.
Frequently asked questions
Can you use implicit differentiation for the second derivative?
Yer, you can use implicit differentiation for the second derivative. To do this, you need to calculate the first implicit derivative and then differentiate it again to get the second implicit derivative of a function.
How do you find the second implicit derivative?
It is very simple to calculate the second implicit derivative. A function is differentiated twcie implicitly to calculate the 2nd implicit derivative. You can also use the following steps.
- Find the first derivative of a function by differentiating both sides.
- Now simplify and rearrange the obtained expression to get dy/dx.
- Find the second derivative by differentiating the first implicit derivative.
- Again simplify and rearrange to get a second derivative.
Why is implicit differentiation used?
When you need to determine the derivative dy/dx but x and y are not directly related, such as y = f(x), implicit differentiation can be helpful. Instead, it's possible that x and y are related by a more complex expression like sin(x + y) = x, where it may be challenging to express y in terms of x.




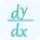
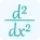
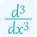












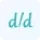
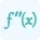
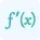
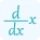


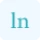

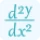
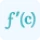



 Google Play
Google Play

0 Comment