Introduction to Implicit Differentiation Calculator?
Implicit differentiation calculator is an online tool through which you can calculate any derivative function in terms of x and y. The implicit derivative calculator with steps makes it easy for beginners to learn this quickly by doing calculations on run time. The step by step results of implicit derivative calculator makes you complete a specific task within minuets.
Integration and differentiation are inverse to each other. You can find useful integration calculators on this website along with useful blogs.
What is Implicit Differentiation?
In Calculus, the word implicit is used for functions which can be expressed as both x and y. Implicit differentiation is a process in which we find the derivative of a dependent variable. It is done by
Separately differentiating the each term
Expressing the derivative of the dependent variable as a symbol
Solving the resulting expression for the symbol.
Formula used by Implicit Differentiation Calculator
The implicit differentiation calculator with steps uses the below formula:
$ x^2 + y^2 = 1 $ $ \frac{d}{dx} \left( x^2 + y^2 \right) = \frac{d}{dx} (1) $
Benefits of using Implicit Function Calculator
It is always very beneficial to use an online tool over a manual method. Some of the top benefits of dy/dx calculator with steps is as follows:
- It saves your time you spend on doing manual calculations.
- Implicit calculators are simple and easy to use.
- It provides accurate and step by step results.
- You can see the plot and possible intermediate steps of implicit differentiation.
- Implicit derivative calculators with steps helps you practice online to consolidate your concepts.
Benefits of using dy dx Calculator
It is always beneficial and smart to use a second implicit derivative calculator with steps for learning and practice. Some of the major benefits of this implicit differentiation solver are:
- It saves your time you spend on doing manual calculations.
- This implicit calculator with steps is simple and easy to use.
- You can do practice to consolidate your implicit differentiation concepts.
- It provides step by step accurate results.
- You can find plot and possible intermediate steps of implicit differentiation.
- You don't need any fee or subscription to use implicit function derivative calculators.
How to use an Implicit Differentiation Calculator?
Our implicit differentiation calculator with steps is very easy to use. Just follow these steps to get accurate results. These steps are:
- Enter the function in the main input or Load an example.
- Select the variable with respect to which you want to evaluate.
- Confirm from preview whether the function or variable is correct.
- Click on the "CALCULATE" button to get a step by step answer.
Frequently Asked Questions
Is implicit differentiation the same as partial differentiation?
In implicit differentiation, the function is differentiated with respect to one variable but the other variable vanishes in the end.
Whereas in the partial differentiation, the function is differentiated with respect to two variables at a time. Use implicit partial derivative calculators to get accurate results online.
What is the derivative of implicit function?
Implicit differentiation, the function is differentiated with respect to one variable by treating another as the function of the first variable. On evaluation, the second variable is isolated from the solution. You can use derivatives of implicit function calculators to get instant and accurate results.
What is the implicit function in differentiation?
A function is called an implicit function if one of its variables is written in the form of another variable. For example, x2+xy=0 is an implicit function because one variable is dependent, that is the function of an independent variable. Meanwhile, you can calculate these functions and equations by using implicit function derivative calculators step by step.
How to find the derivative of implicit function?
We can differentiate an implicit function easily. For example, to find y’ for xy=1, we can perform the following steps.
xy=1
Since y is a function x so,
$ xy(x) \;=\; 1 \implies y(x) \;=\; \frac{1}{x} $
Applying derivative,
$ \frac{d}{dx} \left( xy(x) \right) \;=\; \frac{d}{dx} 1 $ $ 1 y(x) + xy(x) \;=\; 0 $ $ xy(x) \;=\; -y(x) $ $ xy(x) \;=\; \frac{-1}{x} $ $ \implies y(x) \;=\; \frac{-1}{x^2} $




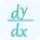
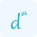
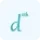
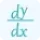












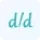
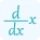






 Google Play
Google Play

0 Comment