Introduction to Derivative at a Point Calculator
A derivative calculator is an online tool that allows you to calculate a derivative at a given point of the function without solving the long-term calculations. It uses the function value as an input and an interval at which you want to calculate the rate of change of that function.
In calculus, the Derivative at a point is an important concept that finds the rate of change of any function. It approximates the given function at the end of change. We introduce a tool online that helps you to calculate derivatives at a given point on the tangent line.
Derivative at a point Calculator with Steps Formula
The derivative at a point refers to approximating a function on a point. In this differentiation, we first find the derivative of the function and then substitute the point in it.
Formula
Let f be a function and there is a point x=a in the domain of f(x). Then the derivative of f(x) with respect to the point x=a is,
$ f'(a) \;=\; \frac{f(a+h)-f(a)}{h} $
Where,
f'a= Derivative at a.
Derivative at a point calculator uses this formula to approximate a given function with respect to the point.
Derivative at a Point example
Let's calculate the derivative of sqrt x at x=4. For this suppose that,
$t=\sqrt{x}$
Differentiating both side with respect to x.
$\frac{dy}{dx}=\frac{d}{dx}(\sqrt{x})$
Using the power rule of derivative.
$\frac{dy}{dx}=f'(x)=\frac{1}{2}x^{\frac{1}{2}-1}\frac{d}{dx}(x)$
$f'(x)=\frac{1}{2}x^{-\frac{1}{2}}=\frac{1}{2\sqrt{x}}$
At x=4,
$f'(4)=\frac{1}{2\sqrt{4}}$
Hence the derivative of sqrt x at x=4 is,
$f'(4)=\frac{1}{2(2)}=\frac{1}{4}$
How to Find Derivatives at a Point Online Calculator?
It is not difficult to find this tool online. You can search it from your browser. It is available on the calculator website. There are also a variety of different mathematical tools on this website. You can also simply use our website URL to access the website.
How does the Derivative at a Point Calculator work?
The working of this calculator depends on the input function and the point where the function's value is to be calculated. It uses the fundamental differential formula to calculate the rate of change in a function at a specific point. It executes fast and provides you a step-by-step complete solution.
When you input a function in this calculator, it analyzes the function and the variable by which you want to find the rate of change. After this, it calculates the derivative of the function and inputs the given point in it to find the value of rate of change at that point.
Why use Derivatives at a Point Formula Calculator?
The Derivative at a point and the ordinary Derivative are two confusing but essential concepts for students. This concept helps to find the slope of a tangent line to a function’s graph at a point. Therefore, it has many applications in mathematics and physics. For example, finding the slope at a certain point is done by finding the Derivative at that point.
You can get confused with the formula when calculating the Derivative at a point by manual calculations. It is because the ordinary Derivative and the Derivative at a point consist of almost the same formulas. There is only a little difference, which makes it confusing for students. Therefore, you need to use this tool to avoid confusion. If you want to find derivatives of extreme points quickly you can also use online extreme point calculator.
Benefits of using Second Derivative at a Point Calculator
Today according to the latest technology updates, it is required that we should update our learning methods with it. So, by following this requirement, we offer you a second derivative at a point calculator that can provide you with many advantages not only in your studies but also in improving your problem-solving skills. Some of these advantages are highlighted below.
- It is a free online tool for you. It does not require any account or a paid subscription plan.
- Derivatives at a point calculator can save your time and energy from solving tricky calculations by hand.
- It provides you fast and 100% accurate results.
- You can find derivatives at any point without learning any manual guide because it is easy to use.
- You can find highly accurate derivatives at a point up to 9th order.
How to use Derivatives at a Point Calculator with Steps?
It is not difficult to find derivatives at a point using this tool because it provides you with an easy and fast solution to your mathematical problems. There are some simple and easy steps to use this tool. These are:
- Write the value of the function in the “Enter Function.”
- Select the order of derivatives from the “computes with.”
- Now select the point from the “When x=.”
- Click on the “Calculate button after reviewing the function that appears when you insert the input value.
You will get the solution within a minute of clicking the calculate button.
Frequently asked questions
What is the derivative formula?
Let f(x) be a function, the derivative of f(x) calculates the rate of change with respect to an independent variable. Then the derivative formula is;
$ f'(x) \;=\; \frac{f(x+δx)-f(x)}{δy} $
How do you find the derivative at a point?
You can calculate the derivative at a point for a function f(x) at x=a by using the following formula,
$ f'a \;=\; \frac{f(a+h)-f(a)}{h} $
Let fx=2 x 3+1, to calculate its derivative at x=2 , We will use the following steps.
$ f(x) \;=\; 2x^3 \;+\; 1 $
Applying derivatives of both sides with respect to ‘x’.
$ f'(x) \;=\; \frac{d}{dx} (2x^3 \;+\; 1) $ $ f'(x) \;=\; 2×3x^{3-1} \frac{d}{dx} (x) \;+\; \frac{d}{dx} (1) $ $ f'(x) \;=\; 6x^2 $
So derivative at x=2,
$ f'(2) \;=\; 6(2)^2 \;=\; 6(4) $ $ f'(2) \;=\; 24 $
What is the significance of finding the derivative at a specific point in a function?
The derivative of a function at a point refers to the rate of change at a point in its domain. It is the measure of how quickly a function changes at a specific point. Finding the derivative of a function at a point is important because it is used to analyze it's behavior and the slope of a tangent line.




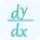
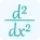
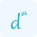
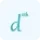
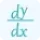












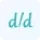
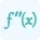
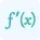
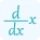






 Google Play
Google Play

0 Comment