Introduction to the Jacobian Matrix Calculator
The Jacobian Matrix plays a fundamental role in mathematics and physics, particularly in the field of multivariable calculus. This powerful tool helps us understand how changes in one set of variables affect another set of variables. Whether you're a student studying calculus or a professional working with complex mathematical models, having a reliable Jacobian Matrix calculator can significantly simplify your calculations. In this article, we will explore the concept of the Jacobian Matrix, discuss its formula, understand its applications at a point, and learn how to effectively use an online Jacobian Matrix calculator.
Formula Used by the Jacobian Matrix with Steps
The formula for calculating the Jacobian Matrix involves partial derivatives. Given a function with multiple variables, the Jacobian Matrix represents the collection of all its partial derivatives. Let's consider a function f with variables x1, x2, ..., xn. The Jacobian Matrix J of f is defined as follows:

For example, let's calculate the Jacobian Matrix for the function f(x, y) = x^2 + y^3:
Determining the function and variables
f(x, y) = x^2 + y^3
Now Computing the partial derivatives:
∂f/∂x = 2x
∂f/∂y = 3y^2
Arrange the partial derivatives in a matrix:
J = | 2x 3y^2 |
Therefore, the Jacobian Matrix for f(x, y) = x^2 + y^3 is J = | 2x 3y^2 |.
How does the Jacobian Matrix at a point work?
To understand the functioning of the Jacobian Matrix, it's essential to understand the concept of a point in mathematics. In the context of multivariable calculus, a point refers to a specific set of values assigned to the variables in a function. The Jacobian Matrix evaluated at a point provides crucial information about the local behavior or continuity of the function around that point.
By analyzing the entries of the Jacobian Matrix, you can determine the rate of change of each component of the vector function concerning the variables at the specified point. This knowledge helps in examining the behavior of the function near that point, such as whether it is expanding or contracting, and in what direction.
How to Use Jacobian Matrix Calculator with Steps?
Using a Jacobian Matrix calculator simplifies the otherwise tedious process of manual computation. Here's a step-by-step guide to utilizing a Jacobian Matrix calculator:
- Access a reliable Jacobian Matrix calculator online.
- Enter the vector-valued function you want to analyze.
- Specify the variables with respect to which you want to calculate the derivatives.
- Click the "Calculate" button to obtain the Jacobian Matrix.
- Review the resulting matrix, which represents the partial derivatives of the function.
Let's consider an example to illustrate the usage. Suppose we have a vector-valued function f(x, y) = (x^2, sin(y), 2xy). To find the Jacobian Matrix at a point (2, π), follow the steps above using the calculator. The resulting Jacobian Matrix will provide insights into the local behavior of the function around the specified point. Use our partial differentiation calculator to find derivatives of a multivariable function.
Why to use Jacobian Matrix Online?
There are several benefits to using an online Jacobian Matrix calculator. Firstly, it provides convenience as you can access it anytime and anywhere with an internet connection. Whether you're studying at home, in a library, or at a coffee shop, you can easily calculate the Jacobian Matrix without the need for complex software installations.
Secondly, online calculators often offer user-friendly interfaces that make the process intuitive and straightforward. Additionally, these calculators are regularly updated, ensuring accurate results based on the latest mathematical algorithms. We also offer you to use the Hessian matrix calculator that involves second-order partial derivatives of the given function.
Benefits of Using Three Variable Jacobian Calculator
The benefits of using a three-variable Jacobian calculator are manifold:
- Widely Applicable in Various Fields: The Jacobian Matrix finds extensive applications in mathematics, physics, engineering, and other scientific disciplines, enabling the analysis of diverse systems.
- Enables Analysis of Complex Systems: By providing insights into the local behavior of functions, the Jacobian Matrix facilitates the study and comprehension of complex systems, aiding in decision-making and problem-solving processes.
- Simplifies Multivariable Calculus: Calculating the Jacobian Matrix for functions with multiple variables can be intricate. Using a dedicated calculator streamlines the process, allowing users to focus on the interpretations and applications of the results.
How to Find a Jacobian Calculator Online?
When searching for a Jacobian matrix calculator online, consider the following steps:
- Start by conducting a web search using relevant keywords, such as "Jacobian matrix calculator" or "online Jacobian calculator."
- Evaluate the credibility and reliability of the calculators by looking for reviews or testimonials from other users.
- Check if the calculator supports the number of variables required for your specific function.
- Ensure that the derivative calculator provides a user-friendly interface and clear instructions for inputting the function and variables.
- Verify if the calculator offers additional features, such as visualization options or the ability to save and export results.
- Choose a calculator that best suits your needs and preferences, taking into account factors like user experience, functionality, and accessibility.
By following these steps, you can find a suitable online Jacobian matrix calculator that meets your requirements.
Frequently Asked Questions
What are some real-world applications of the Jacobian matrix?
The Jacobian matrix finds applications in fields such as physics, engineering, robotics, and economics. It is used in studying fluid dynamics, optimization problems, control systems, and more.
Can the Jacobian matrix be used for optimization problems?
Yes, the Jacobian matrix plays a crucial role in optimization problems. It helps identify critical points, evaluate the stability of solutions, and determine the direction of improvement.
Are there limitations to using online Jacobian matrix calculators?
While online Jacobian matrix calculators are convenient and accurate, they may have limitations in handling extremely complex functions or high-dimensional systems. In such cases, manual or specialized software-based computations may be more suitable.




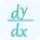
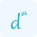
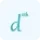
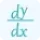












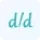
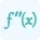
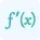
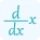






 Google Play
Google Play

0 Comment