Introduction to the Fourth Derivative Calculator
The fourth order derivative calculator is a powerful online tool designed to calculate the fourth derivative of a function. Simplify the process of finding the rate of change of a function with just a few clicks. Input your function and the respective variable to get accurate results.
Understanding Calculus: Derivatives and Integration
Calculus revolves around two fundamental concepts: derivatives and integration. Derivatives measure the rate of change of one quantity with respect to another. There are instances where you need to calculate the rate of change of a function up to four times, which can be a time-consuming and challenging process. To simplify this, we have developed an online tool that allows you to calculate derivatives easily.
How the Fourth Order Derivative Calculator Works
Our fourth derivative calculator employs a derivative formula that enables the calculation of derivatives up to the fourth order. The fourth derivative of a function indicates sudden changes in the function's rate of change, whether it increases or decreases abruptly. The formula used is as follows:
$f'(x)=\lim_{x\to0}\frac{f(x+\delta x)-f(x)}{\delta x}$
For the fourth order derivative:
$f''''(x)=\frac{d^4y}{dx^4}$
The derivative of a function helps determine the slope of a curved line, which represents the rate of change within the function. Our advanced math calculator utilizes the above formula to provide quick and accurate solutions, eliminating the need for manual calculations.
Example of Calculating the Fourth Derivative
Let's calculate the fourth derivative of e^-2x. Assuming:
$y=e^{-2}$
By differentiating both sides with respect to x, we obtain:
$\frac{dy}{dx}=\frac{d}{dx}(e^{-2x})$
Since the derivative of an exponential function is itself an exponential function, we have:
$\frac{dy}{dx}=-2e^{-2x}$
Thus, the first derivative of e^-2x is -2e^-2x. However, our goal is to calculate the fourth derivative, so we will differentiate e^-2x four times. Differentiating the first derivative, we get:
$\frac{d}{dx}\left(\frac{dy}{dx}\right)=\frac{d}{dx}(-2e^{-2x})$
$\frac{d^2y}{dx^2}=4e^{-2x}$
Similarly, the third derivative of e^-2x will be:
$\frac{d^3y}{dx^3}=-8e^{-2x}$
Finally, by differentiating the third derivative of e^(-2x), we obtain the fourth derivative:
$\frac{d^4y}{dx^4}=16e^{-2x}$
Using the Fourth Degree Derivative Calculator
The derivative calculator offers a range of online tools to help you delve deeper into derivatives. Among these tools is the fourth order derivative calculator, which you can easily access online. To find this calculator, follow these steps:
- Use relevant keywords in your search engine of choice to find the desired tool.
- Review the search results and select the fourth implicit derivative calculator that best suits your needs.
- On the website page, you will find a list of derivative tools.
- Choose the fourth order derivative calculator from the list. Alternatively, you can explore other tools such as the extreme point calculator, which helps calculate maximum and minimum points.
- Functionality of the Fourth Order Derivative Calculator
The fourth order derivative calculator works based on the provided input function. It utilizes the fundamental differentiation formula to determine the rate of instantaneous change in the function. The calculator provides a step-by-step solution for finding the fourth derivative by differentiating the function four times.
When you input a function into the derivative calculator, it first analyzes the function and then performs four successive differentiations. While calculating the fourth-order derivative can be a lengthy process, our derivative tool ensures a quick and accurate solution.
Benefits of Using the Fourth Order Derivative Calculator
This calculator offers numerous benefits when used online. Here are some advantages:
Ease of use
The calculator requires only a few simple steps to operate.
Step-by-step solution
It provides a straightforward, step-by-step solution without the need for manual calculations.
Free online tool
Our calculator is completely free, eliminating the need for premium alternatives.
Accurate results
The calculator guarantees 100% accuracy in its results.
Learning opportunities: By using this calculator, you can gain a better understanding of how to calculate the fourth derivative of a function, including the utilization of the chain rule.
Utilizing the 4th Derivative Calculator
Using this online calculator to calculate the rate of change of a function for the second or fourth time is a quick and easy process. It requires input values for calculation. Follow these steps to utilize the calculator effectively:
Enter the function you want to analyze as the first step. Provide the necessary function for which you need to calculate the rate of change four times.
Select the variable by which you want to differentiate the given function.
Review the function and click the calculate button.
Within a few seconds, you will receive the solution. Additionally, you can calculate the rate of change of a function at a specific point using the derivative at a point calculator.
Frequently Asked Questions
What does the fourth derivative tell you?
The fourth-order derivative of a function reveals the sudden rate of change at specific points. It indicates the rate of change in the "jerk" part of acceleration, such as moments when acceleration rapidly increases, like an elevator ascending quickly.
How do you find the fourth derivative?
Finding the second, third, fourth, or higher derivatives is relatively straightforward. The second derivative of a function is the derivative of its first derivative. The third derivative is the derivative of the second derivative, and so on.
What do second derivatives tell us?
The second derivative of a function provides information about the rate of change of its first derivative. The sign of the second derivative indicates whether the slope of the tangent line is increasing or decreasing.




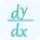
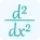
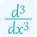
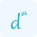
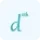
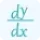












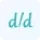
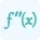
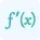
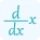


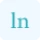

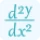



 Google Play
Google Play

0 Comment