Introduction of nth Derivative Calculator
A higher order derivative calculator is an online tool that helps to make your calculations easy while calculating the nth derivative of a function. It allows you to compute the results of a function up to nth order with a complete and step-by-step solution.
The derivative is an essential concept in calculus mainly used to calculate the rate of change. But when calculating higher order derivatives, you may be stuck between the problems because of long-term calculations. Therefore, we introduce you to a tool of maclaurin series calculator that can help you find a function's derivative up to n times.
Formula used by Higher Order Derivative Calculator
The nth derivative refers to applying differentiation n times on the given function. The general formula to calculate derivative of a function n times is:
$ f^n (x) \;=\; \frac{d^n}{dx^n} [f(x)] {2}lt;/p>
This 100th derivative calculator uses the above formula to find derivative n times. You can find the first, second, third, fourth and so on to the nth derivative of any function by using our tool.
Sometimes, when you need to calculate higher order derivatives, you need to follow product and quotient rules also. The derivative calculator successively uses all derivative formulas that are:
- Product rule,
- $ \frac{d^n}{dx^n} {f(x)g(x)} \;=\; f(x).g^n (x) \;+\; f^n (x).g(x) {2}lt;/li>
- Quotient rule,
- $ \frac{d^n}{dx^n} \left(\frac{f(x)}{g(x)} \right) \;=\; \frac{f(x).g^n (x)-f^n (x).g(x)}{[g(x)]^2} {2}lt;/li>
- Power rule,
- $ \frac{d^n}{dx^n} (x^m) \;=\; mx^{m-1} \frac{d^n}{dx^n} (x) {2}lt;/li>
nth Derivative example
Let's calculate the nth derivative of e^x. For this, suppose that,
$y=e^{x}{2}lt;/p>
We will calculate the nth derivative by calculating all derivatives one-by-one. So, for the first derivative, differentiate y with respect to x one time.
$\frac{dy}{dx}=\frac{d}{dx}(e^{x}){2}lt;/p>
$\frac{dy}{dx}=e^{x}{2}lt;/p>
Similarly, differentiate the first derivative to get the second derivative of e^x.
$\frac{d^2y}{dx^2}=\frac{d}{dx}(e^{x})=e^{x}{2}lt;/p>
Similarly, the third derivative will be,
$\frac{d^3y}{dx^3}=^{x}{2}lt;/p>
By continuing this process, the nth derivative will be,
$\frac{d^ny}{dx^n}=e^x{2}lt;/p>
How to find the nth Derivative Calculator Online?
Finding an online tool to calculate the derivative of a function requires some simple steps. These steps will help you to access the nth order derivative calculator easily.
- Open your desired browser and navigate it to the search engine google.
- On Google search bar, search for the derivative calculator. It will provide you with a list of the websites offering tools to calculate derivatives.
- Select our differential calculator from the list.
- On this website, you will find a list of derivative tools. You can also select any of the choices other than the nth order calculator.
How is the nth Derivative Solver?
The nth derivative of a function calculator works when an input function is provided. It uses the fundamental formula of differentiation in the backend to find rate of change. It differentiate a function n times to find nth derivative and provides you a complete step-by-step solution.
When you provide an input function in this calculator, it first analyzes the function to check that either the function is differentiable n times or not. Then, it applies the derivative formula on the function and provides you its nth derivative.
How to use nth Derivative Function Calculator?
The higher order derivative calculations for any function are long and tricky. This calculator gives a solution to this problem by providing you with a step-by-step method to use it. These steps are:
- Write the function value in the “Enter Function.”
- Choose the variable from “with respect to” by which you want to differentiate the function.
- Select the order of derivatives from “Times.”
- Review the function below and click on the calculate button.
As you click the calculate button, the calculator will solve the given problem within a few seconds. It will provide a complete detailed solution to make it understandable.
Why use Higher-Order Derivatives Calculator & Solver?
You are already aware of the importance of derivatives in calculus. Nth order derivative is an advanced term of derivative that has many applications in calculus and applied sciences. The higher order derivatives of a function provide information about it, such as its instantaneous rate of change. For example, the second derivative can measure the acceleration of a moving body.
Benefits of Maclaurin Series Calculator
This tool has many beneficial uses for students and mathematicians. These are:
- The nth derivative calculator is an online free calculator that does not demand any fee or account to sign up.
- It is easy to use; all you do is write the function value and click the calculate button.
- This tool can find the derivative of any function up to nth order with 100% accurate results.
- You can also solve Taylor’s and Maclaurin series for any function with higher order derivatives.
- Higher order derivative calculator is best in all ways and provides easy and step-by-step results.
Frequently asked questions
What is the nth order derivative?
When you apply the differentiation on a function n times, for example 4 or 5 times, this process is called nth order differentiation and the resulting solution is known as nth order derivative. For example, a second order derivative provides acceleration of a moving object with the help of a second derivative calculator.
What is the Leibniz formula?
The Leibniz formula is based on the nth derivative of two functions. It states that if two functions f(x) and g(x) are differentiable n times, then their product follows the product rule of derivative with nth order. Such as:
$ \frac{d^n}{dx^n} {f(x)g(x)} \;=\; f(x).g^n (x) \;+\; f^n (x).g(x) {2}lt;/p>
In generalized form,
$ \frac{d^n}{dx^n} {f(x)g(x)} \;=\; \sum_{k=0}^n f^{n-k} (x)g^k (x) {2}lt;/p>
What is the nth derivative of constant?
The derivative of a constant like 1, 2 or 3 is always equal to zero. It means that if we apply the derivative formula on a constant n times, it will still be equal to zero. Hence the nth derivative of a constant is zero.




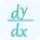
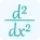
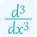
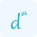
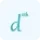
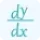












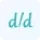
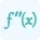
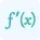
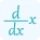



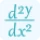
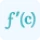



 Google Play
Google Play

0 Comment