Introduction to Limit L'Hopital's Rule Calculator
Welcome to the l'hopital calculator, your go-to online tool for effortlessly solving limits using L'hopital's rule. Whether tackling complex mathematical problems or trying to find the limit of a challenging function, this calculator provides step-by-step guidance to help you navigate the process with ease. This article aims to provide a clear understanding of what L'Hospital's Rule entails, how the calculator employs a specific formula to address problems, and how you can effectively use it.
How L'Hôpital's Rule Calculator works?
Now that we understand the formula, let's explore how l hospital rule calculator harnesses this principle to simplify the process. This online tool is designed to perform the derivative calculations efficiently, eliminating the need for manual, time-consuming differentiation.
Here's a basic overview of how it works:
Step 1: Input your limit equation into the calculator, specifying the variable (usually x) and the value of the limit (c) as required.
Step 2: The calculator identifies if the limit is indeterminate (0/0 or ∞/∞).
Step 3: It then automatically calculates the derivatives of the numerator and denominator functions using the power of calculus.
Step 4: The tool continues this process iteratively until a determinate form is achieved.
Step 5: Finally, it provides you with the simplified limit value.
Steps to Evaluate Limits Using L'hopital's Rule
- Enter the given function and the limit value you want to evaluate.
- The calculator will analyze the function and check for indeterminate forms (0/0 or ∞/∞).
- If an indeterminate form is detected, the calculator calculates the derivatives of the numerator and denominator.
- It then simplifies the ratio of the derivatives and calculates the limit of the simplified expression.
- The calculator presents you with the final limit value along with detailed step-by-step explanations.
Formula Used by L'Hopital's Rule Calculator with steps

The formula used by L'Hôpital's Rule, which helps evaluate limits involving indeterminate forms, is as follows:
If you have an indeterminate form of the type \(\frac{0}{0}\) or \(\frac{\infty}{\infty}\) when evaluating the limit of a function. This rule states that:
\[ \lim_{{x \to a}} \frac{{f(x)}}{{g(x)}} = \lim_{{x \to a}} \frac{{f'(x)}}{{g'(x)}} \]
where both f(x) and g(x) are differentiable functions and satisfy the conditions:
\(\lim_{{x \to a}} f(x) = 0\) and
\(\lim_{{x \to a}} g(x) = 0\) or
\(\lim_{{x \to a}} f(x) = \infty\) and
\(\lim_{{x \to a}} g(x) = \infty\)
Additionally, it's important to note that f'(x) and g'(x) are the derivatives of the respective functions with respect to x.
L'Hôpital's Rule essentially allows you to simplify the evaluation of certain limits involving fractions of functions that approach 0/0 or ∞/∞ by taking the derivatives of the numerator and denominator separately and then evaluating the limit of their ratio.
Benefits of Using L'Hopital Calculator
Efficiency: The calculator handles complex limit evaluations that can be time-consuming when done manually.
Accuracy: Algorithms ensure precise determination of limits using L'hopital's rule, minimizing errors.
Step-by-Step Guidance: The calculator provides a breakdown of each step taken, aiding in understanding.
Varied Scenarios: It accommodates a wide range of functions and limits problems, making it versatile.
Frequently Asked Questions
Can the l'hopital's rule calculator with steps handle limits involving trigonometric functions?
Absolutely. The L'hopital's Rule Calculator is equipped to tackle limits involving various types of functions, including trigonometric functions.
Is this calculator suitable for students new to calculus?
Yes, the calculator is designed to be user-friendly and accessible for calculus learners. It provides clear explanations for each step.
How accurate are the results provided by the l hospital rule calculator?
The calculator employs precise mathematical principles, ensuring accurate results for your limit evaluations. However, it's important to input the correct function and limit values for accurate solutions.
How can I interpret the final limit value provided by the calculator?
The final limit value represents the behavior of the function as the input approaches a specific value. It indicates whether the function approaches a constant value, infinity, or negative infinity as the input gets closer to the specified point.




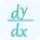
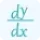












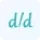
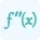
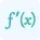
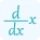



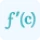



 Google Play
Google Play

0 Comment